Kinematika kmitavého pohybu
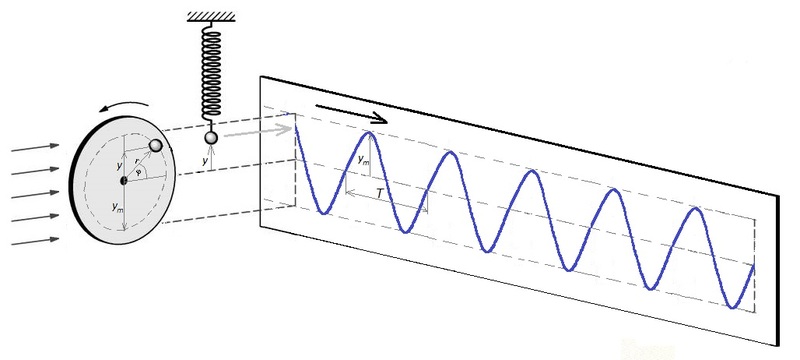
Obr. 1: Souvislost kmitavého pohybu s pohybem rovnoměrným po kružnici
Základní pojmy kmitavého pohybu (viz obr. 1):
okamžitá výchylka…y …mění se periodicky s časem, nabývá kladných i záporných hodnot
amplituda výchylky…ym …absolutní hodnota největší výchylky
U kmitavého pohybu lze nalézt analogii s rovnoměrným pohybem po kružnici (viz obr.1).
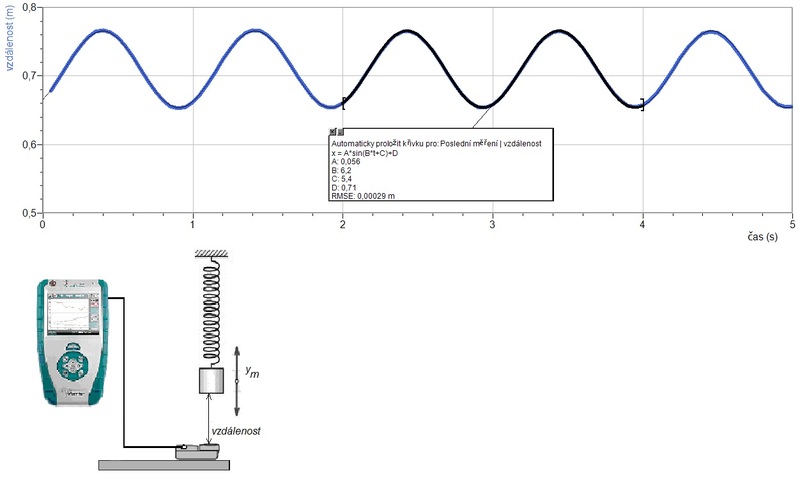
Obr. 2: Časový průběh vzdálenosti (od ultrazvukového měřidla) tělesa na čase
Pro okamžitou výchylku harmonického pohybu platí vztah:

1 radián je středový úhel, který přísluší oblouku o stejné délce, jako je poloměr kružnice r.

Kmitavý pohyb, jehož časovým diagramem je sinusoida (kosinusoida), nazýváme harmonický kmitavý pohyb nebo obecně harmonické kmitání.
Úlohy:
1. Hmotný bod kmitá s amplitudou 4,5 cm a s periodou 0,25 s. Napište rovnici harmonického kmitání.
2. Rovnice harmonického kmitání má tvar y = 6·10-3sin(4πt). Určete:
a) amplitudu výchylky harmonického kmitání
b) jeho frekvenci.
3. Určete dobu od počátečního okamžiku, za kterou hmotný bod kmitající podle rovnice v úloze 2 dosáhne výchylky:
a) – 6 mm
b) 3 mm.
4. Rovnice pro výchylku harmonického pohybu můžeme napsat také ve tvaru y = ymcosωt. Čím se tento pohyb liší od pohybu popsaného rovnicí
y = ymsinωt?
5. Nejtenčí struna kytary vydává tón e1 o frekvenci přibližně 330 Hz. Napište rovnici kmitání bodu uprostřed struny, jestliže jsme střed struny vychýlili o 3 mm. Předpokládáme, že struna kmitá delší dobu se stálou amplitudou.
6. Harmonický kmit je vyjádřen tabulkou:

Napište rovnici výchylky harmonického kmitání. Nakreslete časový diagram kmitání.
7. Změřte frekvenci a periodu kmitavých pohybů na videu.
Rozšiřující pojmy
1 radián je středový úhel, který přísluší oblouku o stejné délce, jako je poloměr kružnice r. Obr. 3: Definice úhlu 1 radiánVideo
Různé kmitavé pohyby




