Složené kmitání
Složené kmitání vzniká, jestliže kmitají současně dva nebo více oscilátorů, které jsou navzájem propojeny vazbou. Vazbu může vytvářet například gumové vlákno nebo pružina (video).
K určení výsledné polohy tělesa můžeme použít princip superpozice:
Jestliže hmotný bod koná současně několik harmonických kmitavých pohybů téhož směru s výchylkami y1, y2, …, yk, je výchylka y výsledného kmitání
y = y1 + y2 + … + yk.
Výchylky mohou mít v určitém okamžiku kladnou i zápornou hodnotu. Proto se při superpozici sčítají a odečítají.
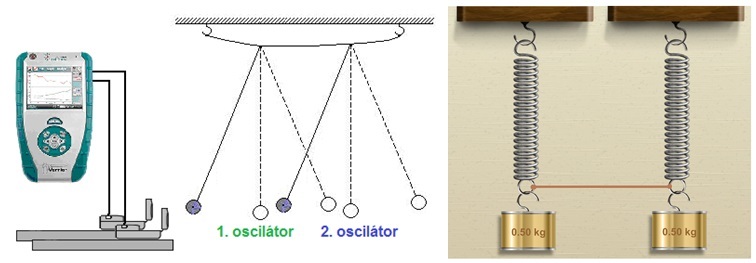
Obr. 1: Demonstrace složeného kmitání – oscilátory jsou spojeny gumovým vláknem
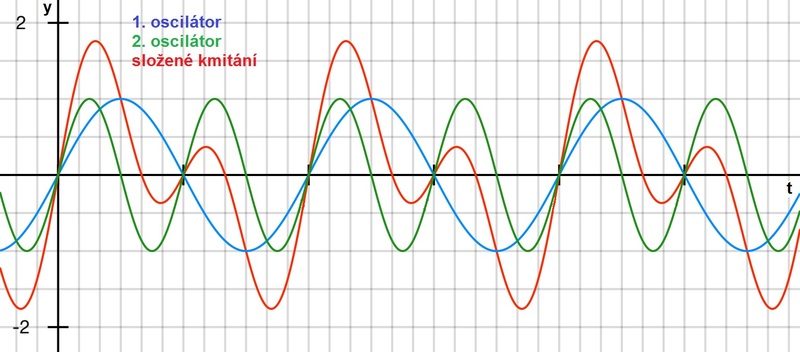
Obr. 2: Složené kmitání dvou harmonických kmitání o stejné amplitudě a různé frekvenci
Superpozice dvou harmonických kmitání s různou amplitudou, stejnou frekvencí a s různým fázovým rozdílem:
a) ve fázi
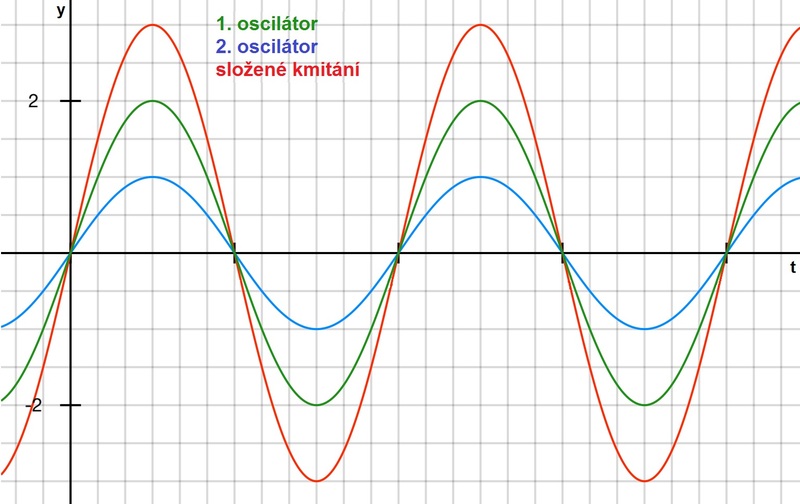
Obr. 3: Superpozice dvou harmonických kmitání s různou amplitudou a stejnou frekvencí
b) s různým fázovým rozdílem
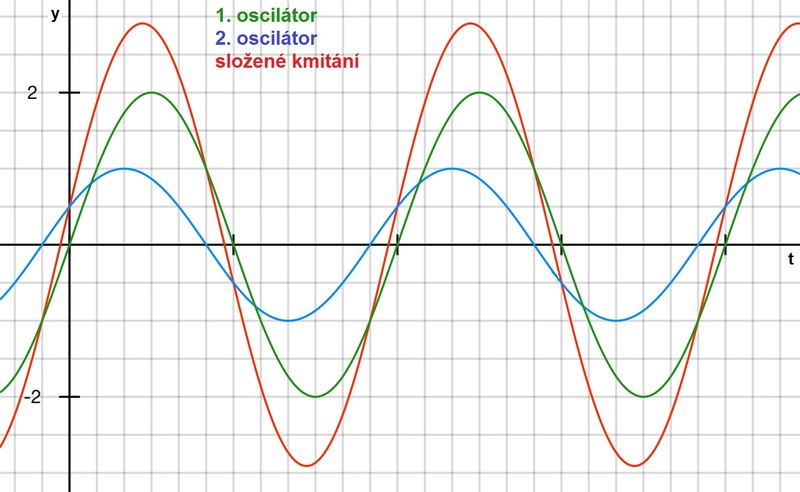
Obr. 4: Superpozice dvou harmonických kmitání s různou amplitudou, stejnou frekvencí a s různým fázovým rozdílem
c) se stejnou amplitudou a s různým fázovým rozdílem
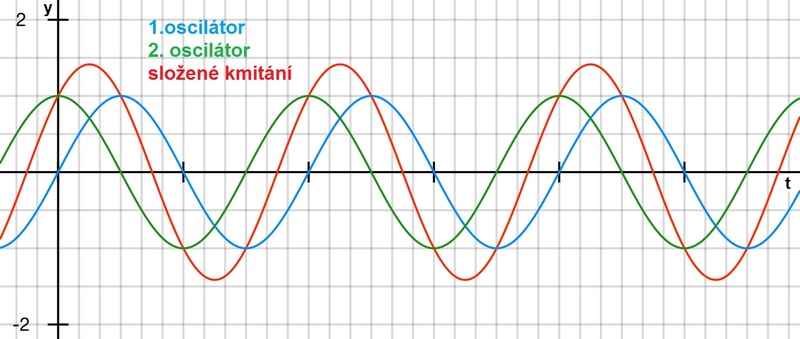
Obr. 5: Superpozice dvou harmonických kmitání se stejnou amplitudou, stejnou frekvencí a s různým fázovým rozdílem
d) s různým fázovým rozdílem
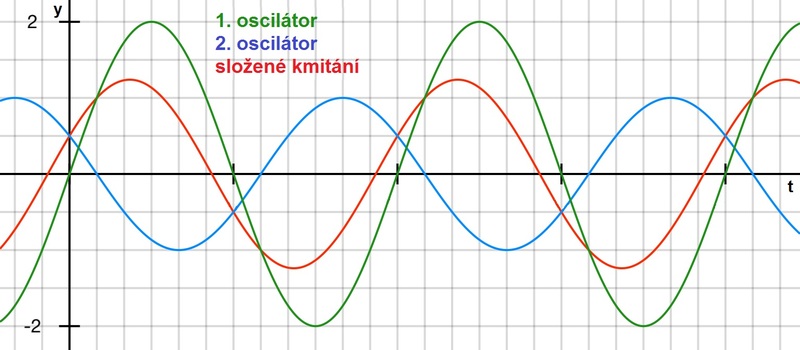
Obr. 6: Superpozice dvou harmonických kmitání s různou amplitudou, stejnou frekvencí a s různým fázovým rozdílem
e) s opačnou fází
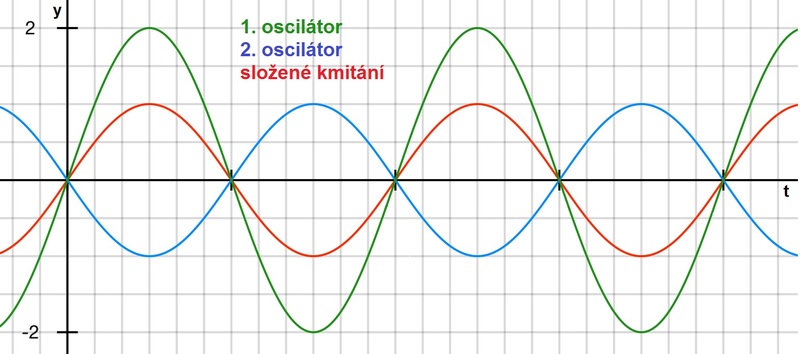
Obr. 7: Superpozice dvou harmonických kmitání se různou amplitudou, stejnou frekvencí a s různým fázovým rozdílem - opačnou fází
Závěr:
Skládáním dvou harmonických kmitání stejného směru a o stejné frekvenci vzniká opět harmonické kmitání téže frekvence (viz a) až e)). Jeho amplituda závisí na fázovém rozdílu složek.
Superpozice kmitání různé frekvence. Složené kmitání není harmonické.
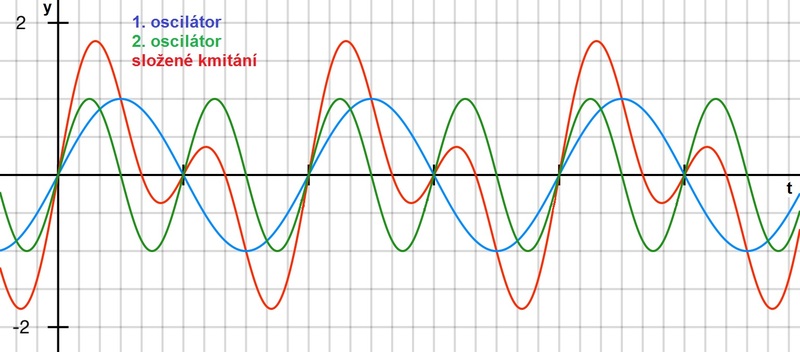
Obr. 8: Superpozice dvou harmonických kmitání s různou frekvencí
Superpozice kmitání blízkých frekvencí. Vznikají tzv. rázy (u zvuku zázněje).
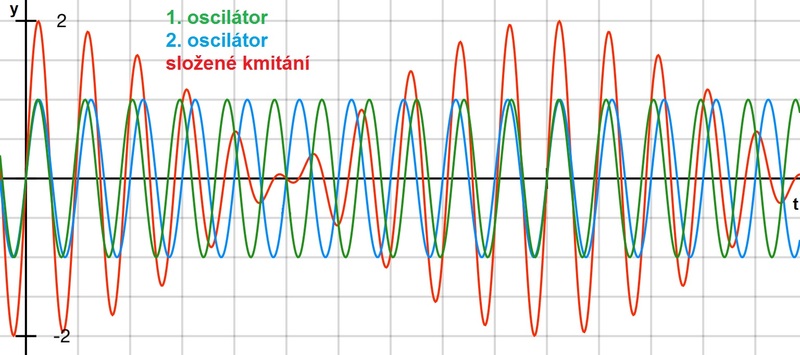
Obr. 9: Superpozice dvou harmonických kmitání s různou frekvencí (s blízkou frekvencí)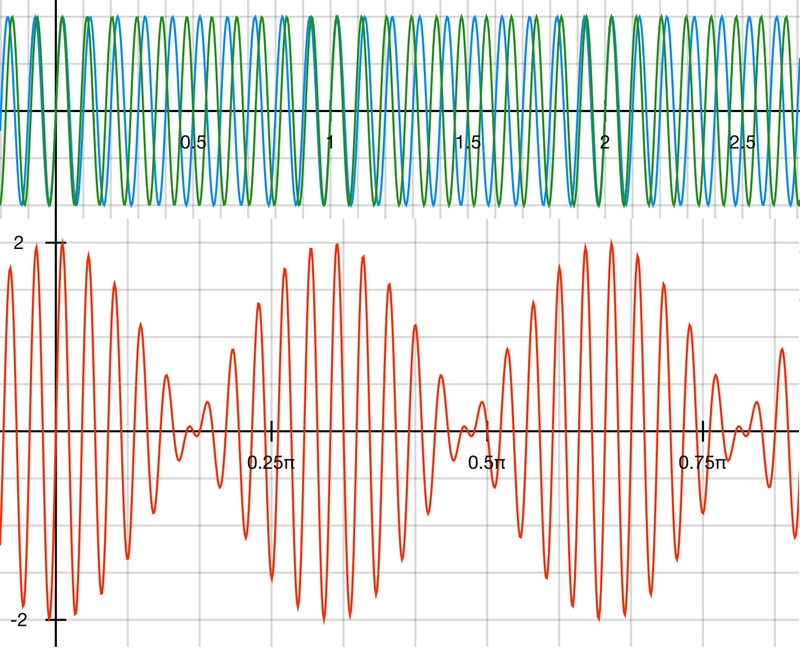 Obr. 10: Superpozice dvou harmonických kmitání s různou frekvencí (s blízkou frekvencí)
Obr. 10: Superpozice dvou harmonických kmitání s různou frekvencí (s blízkou frekvencí)
Frekvence rázů je f = f1 – f2.
Úlohy:
1. Jaký je fázový rozdíl kmitání, pro jejichž výchylky platí rovnice:
y1= ym sin ωt, y2 = -2ym sin ωt? Napište rovnici složeného kmitání. Nakreslete, popř. zobrazte pomocí počítače jeho časový diagram.
2. Zobrazte časové diagramy složek harmonického kmitání, pro které platí: y1= ym sin ωt, y1= ym cos ωt. Grafickou superpozicí určete, v kterém okamžiku dosáhne složené kmitání amplitudy výchylky (dobu vyjádřete zlomkem periody).
3. Napište rovnici složeného kmitání, které jste získali superpozicí v úloze 2.
4. Superpozicí tří harmonických kmitání vznikne kmitání s nulovou amplitudou (kmitání zanikne). Dvě složky jsou popsány rovnicemi y1= ym sin ωt a y2= ym sin (ωt+ 2π/3). Napište rovnici třetí složky.
5. Hudebník nechal rozeznít ladičku o frekvenci 220 Hz a současně svůj nástroj. Získal tak zvukové rázy s periodou asi dvě sekundy. Na jaké frekvenci zní nástroj? Vyzkoušej v programu Soundcard Scope.
Měření M.5 → Složené kmitání
Pracovní list na skládání kmitání (v příloze dole). Proveďte superpozici dvou harmonických kmitání. Doplňte chybějící popis obou os.
Přílohy
Video
Složené kmitání




