Složené spojité regulátory
Složené regulátory jsou tvořeny vhodnou kombinací jednoduchých regulátorů a umožňují dosáhnout vyšší kvality regulace. Ústřední člen složeného regulátoru můžeme realizovat jako paralelní spojení jednoduchých regulátorů. Výhodou tohoto způsobu je, že parametry jednotlivých složek nastavujeme samostatnými prvky, takže se navzájem neovlivňují (regulátor bez interakce), nevýhodou je vyšší počet zesilovačů. Používané kombinace jsou PI, PD, PID.
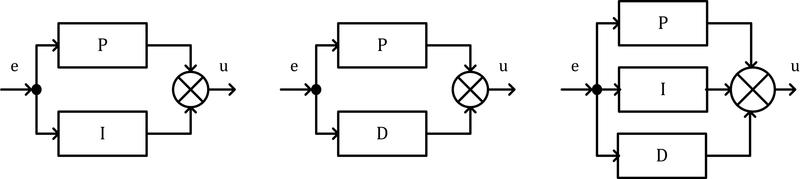
Obr. 1: Bloková schémata složených regulátorů
Součet signálů se provádí invertujícím sumátorem.
Podle blokové algebry platí, že přenosy jednotlivých složek se sčítají.
Regulátor PI – proporcionálně integrační
Chování ideálního regulátoru PI můžeme popsat diferenciální rovnicí
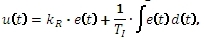
kde kR je zesílení regulátoru a Ti je integrační konstanta.
Z obrazu rovnice
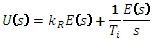
stanovíme obrazový přenos
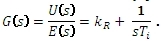
Přechodovou i frekvenční charakteristiku získáme součtem charakteristik jednotlivých složek:
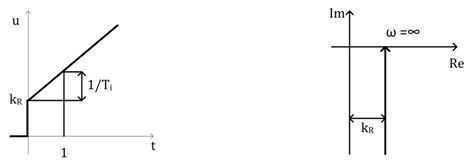
Obr. 2: Přechodová a frekvenční charakteristika regulátoru PI
PI regulátor odstraňuje regulační odchylku. Na začátku regulace převládá vliv proporcionální složky, s narůstajícím časem převládá vliv integrační složky. Na vyšších frekvencích má větší přenos než integrační regulátor, proto reaguje rychleji na nárazové poruchy.
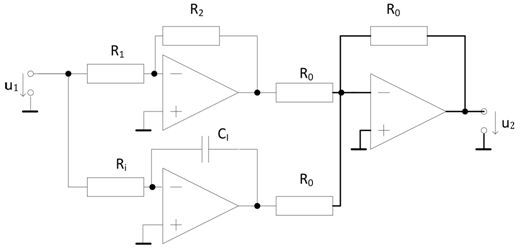
Obr. 3: Zapojení regulátoru PI
Regulátor PD – proporcionálně derivační
Pro ideální regulátor PD platí diferenciální rovnice:
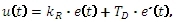
kde kR je zesílení regulátoru a TD je derivační konstanta.
Její obraz v transformaci:
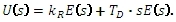
Obrazový přenos má tvar:
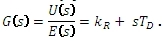
Odpovídající přechodová a frekvenční charakteristika:

Obr. 4: Přechodová a frekvenční charakteristika regulátoru PD
PD regulátor pracuje s trvalou regulační odchylkou. Nejprve převládá vliv derivační složky, později převládá vliv složky proporcionální. Má větší přenos na vyšších frekvencích než proporcionální regulátor, velmi rychle potlačuje časté poruchy. Používá se málo.
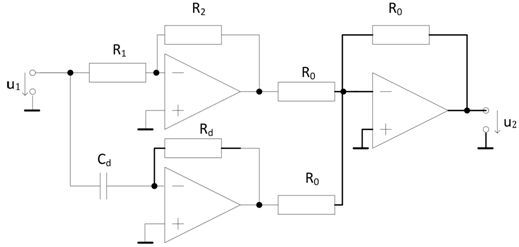
Obr. 5: Zapojení regulátoru PD
Regulátor PID – proporcionálně integračně derivační
Dynamické vlastnosti ideálního regulátoru PID popisuje diferenciální rovnice:
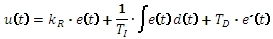
s obrazem
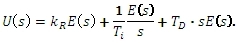
Obrazový přenos:
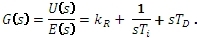
Přechodová a frekvenční charakteristika:
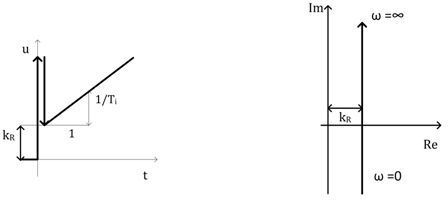
Obr. 6: Přechodová a frekvenční charakteristika regulátoru PID
Na počátku regulace převládá vliv derivační složky, s postupem času převládá složka integrační. Odstraňuje regulační odchylku a rychle kompenzuje časté poruchy.
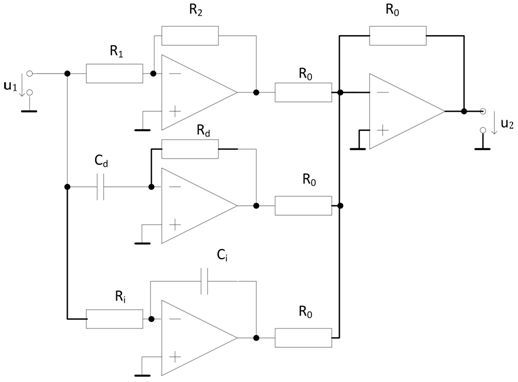
Obr. 7: Zapojení regulátoru PID
Zdroje
-
BALÁTĚ, Jaroslav. Automatické řízení. 2. přepracované vyd. Praha: BEN – technická literatura, 2004, 664s. ISBN 80-7300-148-9.
-
VORÁČEK, Rudolf, František ANDRÝSEK, Zdeněk BRÝDL, Luděk KOHOUT a Ladislav ŠMEJKAL. Automatizace a automatizační technika II. 1.vyd. Praha: Computer Press, 2000, 218s. ISBN 80-7226-247-5.
Obrázky
- Obr. 1, 2, 3, 4, 5, 6, 7 a 8: Archiv autora
Kontrolní otázka
Jak jsou realizovány složené spojité regulátory?
Kontrolní otázka
Jakou výhodu má regulátor bez interakce?
Procvič si
Zakreslete charakteristiky PI regulátoru a uveďte jeho vlastnosti.





