Měření tíhového zrychlení tělesa pomocí matematického kyvadla
Teoretická příprava
Matematické kyvadlo je definované jako těleso zavěšené na nehmotném tuhém závěsu o dané délce. Vytváří tak ideální model kuličky kývající na vlákně o stálé délce. Pokud se experimentálně chceme co nejvíce takovému modelu přiblížit, je nutné použít co nejtěžší kouli na velmi pevném vlákně.
Označíme si hmotnost kývajícího tělesa m a délku závěsu l.

-
Na obrázku kmitá kulička zavěšená na provázku. Její pohyb je způsoben výslednicí tahové a tíhové síly, která na kuličku působí.
-
Tíhová síla je přímo úměrná hmotnosti tělesa, na které působí Země gravitační silou. Vypočítá se podle vztahu:
kde g je konstanta úměrnosti mezi tíhovou silou FG a hmotností m, nazývá se tíhové zrychlení.
-
Jestliže kulička projde postupně třemi krajními polohami, zaujme původní polohu. Doba jednoho kmitu (pohyb kuličky z jedné krajní polohy do druhé krajní polohy a zpět) se nazývá perioda T. Tento pohyb se periodicky opakuje.
-
Pro dobu kmitu T matematického kyvadla platí vztah:
kde l je délka vlákna a g je tíhové zrychlení.Tedy doba kmitu nezávisí na hmotnosti tělesa.
-
Z předešlého vztahu již snadno vyjádříme tíhové zrychlení:
kde π je Ludolfovo číslo (přibližně π=3,14), l je délka provázku a T je perioda.
-
Tabelovaná hodnota tíhového zrychlení připadající na naši zeměpisnou polohu je:
Pomůcky:
ISES, snímač, optická závora, ocelová kulička, pevná nit.

Nastavení ISESu :
-
Doba měření: 10 s
-
Vzorkování: 200Hz
-
Start měření: Manuální
-
Vstupní kanál: Modul světelná závora
Postup práce:
- Ke stojanu upevníme kuličku uvázanou na niti a optickou závoru tak, aby kulička při svém kmitavém pohybu pravidelně přerušovala signál optického čidla.

- Nastavíme parametry ISES systému.

-
Uvedeme kuličku do kmitavého pohybu a přerušení signálu sledujeme na monitoru počítače.
-
Z grafu pomocí zpracování výsledků odečteme doby kmitu kyvadla.
Obr. 5: Odečtení hodnot z grafu
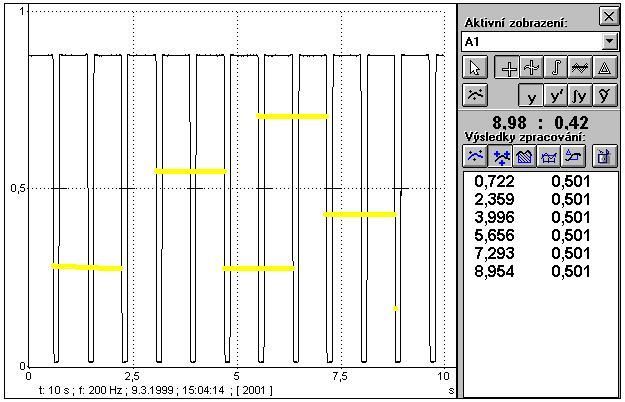
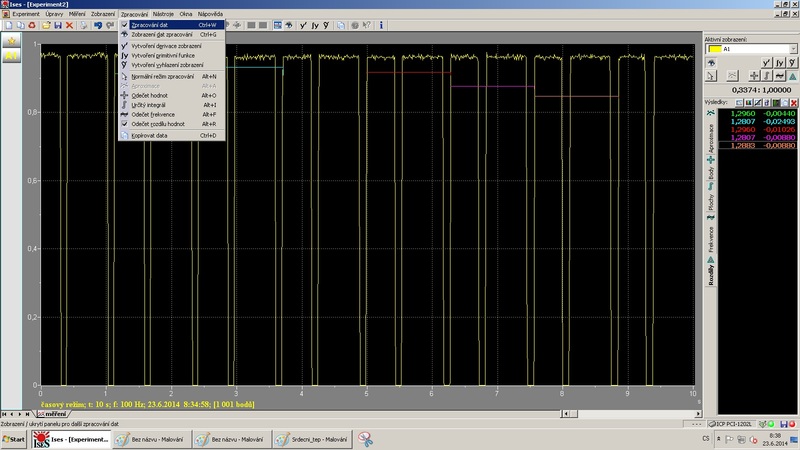 Obr. 6: Odečtení hodnot z grafu
Obr. 6: Odečtení hodnot z grafu
Z těchto hodnot vypočítáme střední hodnotu doby kmitu kyvadla.
-
Vypočítáme střední hodnotu tíhového zrychlení ze vzorce:
-
Hodnotu tíhového zrychlení porovnáme s tabelovanou hodnotou g0 tak, že vypočítáme relativní chybu měření tíhového zrychlení v procentech ze vzorce:

Zdroje
- Fadenpendel. Www.walter-fendt.de [online]. 2014 [cit. 2014-11-29]. Dostupné z: http://www.walter-fendt.de/html5/phde/pendulum_de.htm
- Mechanický oscilátor. Www.youtube.com [online]. 2013 [cit. 2014-11-29]. Dostupné z: https://www.youtube.com/watch?v=PjLzLK7429s
- Matematické kyvadlo. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2014-11-29]. Dostupné z: https://cs.wikipedia.org/wiki/Matematick%C3%A9_kyvadlo
- Christiaan Huygens. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2014-11-30]. Dostupné z: https://cs.wikipedia.org/wiki/Christiaan_Huygens
Obrázky:
- Obr. 1: Kyvadlo. Univerzita Komenského Bratislava: Katedra matematiky, fyziky a informatiky [online]. Bratislava [cit. 2014-11-10]. Dostupné z: http://www.ddp.fmph.uniba.sk/~koubek/UT_html/G3/kap5/5-7.htm
- Obr. 2: archiv autora
- Obr. 3: archiv autora
- Obr. 4: archiv autora
- Obr. 5: archiv autora
- Obr. 6: archiv autora
Přílohy
Protokol
Laboratorní protokol najdete zde.
Úkol
Urči periodu matematického kyvadla z grafu fyzikálního apletu a vypočítej tíhové zrychlení.
Pokus
Na čem závisí perioda matematického kyvadla?
Čti také
Co je to matematické kyvadlo?




